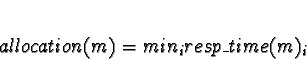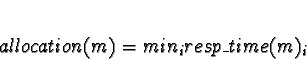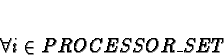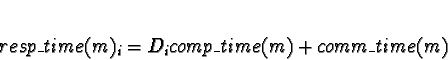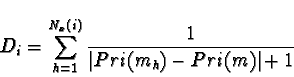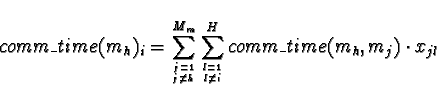


Next: Merge-Sort
Up: Background
Previous: VIA vs. TCP/IP
Although the basic idea of improving computer performance through
parallel processing is simple and obvious, finding the optimal
arrangement for a particular problem and hardware configuration can
easily become an intractable problem. The idea that computation can
be broken into 10 pieces, sent to 10 processors, and execute in 1/10
the time is not realistic. There are many factors affecting overall
processing time, and quite a few models [CCM92,MP98,Gor97,DB99,OR97,Bar98,RR00,JL99,HC97,LS97,AA00,LT00,HC99,GG94,LC99] devised to predict and improve performance in
parallel
systems. Some factors are very difficult to account for accurately when trying to decide how to allocate processes to processors, such as the effects of DMA transfers or processor cache on process execution time.
A solid, common ground starting point is that the total execution time for a job which starts and finishes at single points is the longest execution path between those points[MP98]. Modeling the parts of the path may be a difficult task, but when using experimental measurements this perspective is a good starting point, and can be used to clearly describe why an overall execution time is what it is.
Having a small number of nodes and algorithms that limit the number of
possible configurations greatly simplifies the problem. Our system
allows for a maximum of 8 MPI processes, which is more than sufficient
for creating the fastest configurations on a four processor system.
If each processor is giving its full capability to one process,
breaking the task into more, smaller process will at best take the
same amount of time, and will likely take longer because of the added
overhead of process scheduling, context switching, and fewer cache
hits. This may not be the case for all operating systems and
hardware, but experimental results from our hardware showed that a
dual processor machine took nearly four times as long to complete
three identical processes as it did to complete two. A similar result
was found for passing data over the network: passing one large message
takes less time than passing two messages with half as much data each.
These are important factors to consider, though difficult to model.
Models for dynamic task allocation or load balancing for many programs
also try to take into account the total load and processor capacities
before calculating a load balance. Since our system consisted of four
identical processors, the process distribution was decided before
execution time, and neither workstation was being used for any
particular purpose other than our tests, the load balancing issue was
approached as if all processors were equal and there were no other
load on the system.
Although leaving some processors idle while waiting for data or
synchronization is suboptimal for a general load [Bar98], the
constraints of the algorithms used here do not allow for the
fine-grained data distribution that might lead to full processor
utilization. The problem investigated here is the allocation of
either seven or five processes, for merge-sort and quadtree
compression respectively. Most critical is the allocation of the four
leaf nodes from the virtual tree graph of processes. Theoretical
predictions will be made based on the dynamic allocation algorithms
examined in [DB99], and processor usage graphs
[Bar98].
Briefly, the process allocation algorithm is based on picking the
processor expected to execute of task fastest and allocating the task
to that processor. A task is a computational sub-unit of a program,
after the program has been broken down into parts that can be done in
parallel. The allocation is done at the time a particular task is
ready to run. The point at which a task is ready to run is based on
the application graph, which describes data passing, precedence (a
task precedes another if the first task must complete before the
second can start), and synchronization (two tasks must start at the
same time). The estimate of how fast a processor will execute a task
is based on the current load of that processor, the expected
computation time for that task, and the communication time between
that task and previously allocated tasks, i.e. tasks whose physical
location hasn't been set are ignored. Their equations also attempt to
account for varying processor speeds and processing loads from other
programs. These effects are ignored here since all processors in our
system are the same, and our best a priori guess is that they are
loaded equally. Allocation to each processor of the dual processor
workstations is considered in calculations, although in the actual
system Windows NT controls process allocation within a workstation,
and we only control which workstation a process is allocated to. The
allocation function used to pick a processor number i from the set
of all processors
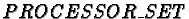 to send task m to is as follows:
to send task m to is as follows:
The simplified function
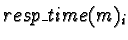 used in this thesis, where
used in this thesis, where
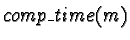 is the
estimated processor time to execute the task and
is the
estimated processor time to execute the task and
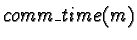 is a
communication delay discussed later, is defined as:
is a
communication delay discussed later, is defined as:
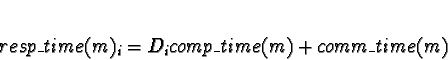 |
(1) |
The value Di is used to account for active tasks already allocated
to processor i, and is calculated to be:
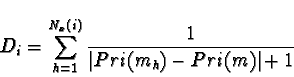 |
(2) |
In this formula, Nx(i) is the set of all tasks currently allocated to processor i, and Pri(mh) is the priority of process mh as determined by a priority scheme where the root has priority 1, tasks preceded by root have priority 2, etc.. Because of the tree structure of the programs examined here, tasks are only allocated along with others of the same priority. This means that, in effect, Di is the number of the tasks already allocated to a processor.
The function
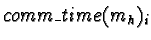 is the sum of all expected data
passing delays between task mh, were it assigned to processor i,
and all tasks already assigned to other processing nodes. Data
passing with tasks on the same node is sufficiently fast that it is
ignored, as are contention for bandwidth on the network, and expected
communications delays with tasks not yet allocated. These factors are
considered by more complex published algorithms, but the amount of
calculation involved increases greatly, and taking these factors into
account would not change the results for the cases considered in this
thesis. That said, the equation accounting for communications delay
is:
is the sum of all expected data
passing delays between task mh, were it assigned to processor i,
and all tasks already assigned to other processing nodes. Data
passing with tasks on the same node is sufficiently fast that it is
ignored, as are contention for bandwidth on the network, and expected
communications delays with tasks not yet allocated. These factors are
considered by more complex published algorithms, but the amount of
calculation involved increases greatly, and taking these factors into
account would not change the results for the cases considered in this
thesis. That said, the equation accounting for communications delay
is:
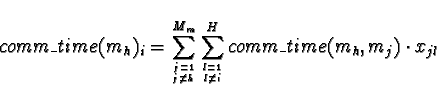 |
(3) |
where Mm is the set of all tasks in the application graph, H is the set of network hosts with tasks allocated to them, xjl is a sort of boolean mask which is equal to one of task mj is allocated to host l, and
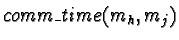 is the expected communication time between mh and mj.
is the expected communication time between mh and mj.
These equations, and the resulting allocations, will be solved and compared to experimental results for each setup. The task allocation graphs don't always correspond exactly to processes assigned to physical resources, since often a single process is responsible for two tasks: one when data is being distributed, and another when data is being gathered back together.



Next: Merge-Sort
Up: Background
Previous: VIA vs. TCP/IP
Garth Brown
2001-01-26